An L-system or Lindenmayer system is a parallel rewriting system, namely a variant of a formal grammar, most famously used to model the growth processes of plant development, but also able to model the morphology of a variety of organisms.[1] A L-system consists of an alphabet of symbols that can be used to make strings, a collection of production rules which expand each symbol into some larger string of symbols, an initial "axiom" string from which to begin construction, and a mechanism for translating the generated strings into geometric structures. L-systems can also be used to generate self-similar fractals such as iterated function systems. L-systems were introduced and developed in 1968 by the Hungarian theoretical biologist and botanist from the University of Utrecht, Aristid Lindenmayer (1925–1989).
The Algorithmic Beauty of Plants by Przemyslaw Prusinkiewicz and Aristid Lindenmayer
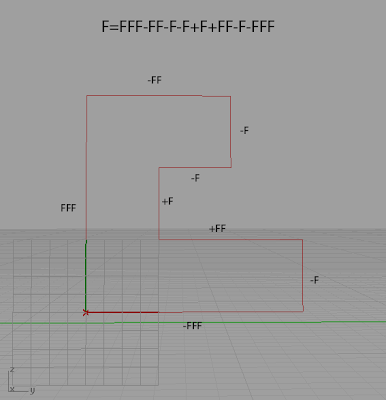
1.3 Turtle interpretation of strings
The geometric interpretation of strings applied to generate schematic
images of Anabaena catenula is a very simple one. Letters of the
L-system alphabet are represented graphically as shorter or longer rectangles with rounded corners. The generated structures are one-dimensional chains of rectangles, reflecting the sequence of symbols in the corresponding strings.
RELATION TO RABBIT
Now to relate this basic understanding to the grasshopper plugin- Rabbit. This is a super simple break down of the definition and what it means when pluged into Rabbit, I'm going to slowly develop this understanding into hopefully making multi-origin branching structures.
Changing the angle in the turtle node effects the final result.